[1]Intro : Some Representative problems

Stable Matching

問題描述

1962年，兩位數學經濟學家David Gale, Lloyd Shapley發起了問題：

Could one design a college admissions process, or a job recruiting process, that was self-enforcing?

他們的疑問究竟是甚麼呢？白話來說，就是指在需要兩兩配對的事情上（例如：應徵工作、結婚），能否設計一套邏輯來配對，並且要stable。你現在一定很疑惑甚麼是stable呢？讓我們以「男女配對」的問題來把整個問題情境敘述地更清楚。

如果你是月老...

現在有2個男生（XY）及2個女生（AB），僅考慮男-女配對的情況，每個人都有自己的偏好順序清單（如下表），要如何設計一方法將兩兩配對，並且stable（穩定）呢？

Stable

stable的意思難以直接解釋，但可以說成Not unstable，而 unstable就是指「在現存的配對中，男、女各自都有更喜歡的人（順序清單上順位較高者）彼此互相喜歡」，以例子說明unstable及stable：

unstable （X-B）、（Y-A），因為X喜歡A>B且A也喜歡X>Y。
stable（NOT unstable ） : （X-A）、（Y-B）。

男生偏好順序	1st	2nd
X	A	B
Y	A	B

女生偏好順序	1st	2nd
A	X	Y
B	X	Y

stable matching不一定只有一種組合

讓我們用不同的偏好順序清單來看看!下面兩種組合都符合stable的定義：

stable（NOT unstable ） : （X-A）、（Y-B）和（X-B）、（Y-A）。

男生偏好順序	1st	2nd
X	A	B
Y	B	A

女生偏好順序	1st	2nd
A	Y	X
B	X	Y

名詞定義

Perfect matching
假設有n男n女，且為一夫一妻制。matching 定義是只要有一堆（<=n）「不相交」的pairs；而Perfect matching是指剛好有n對pairs。
*perfect matching 不一定stable，每個人都有對象，但不一定幸福。
Stability
在配對中的男女沒有動機去破壞已分配好的狀態。
Stable matching
Perfect matching且沒有unstable pairs。
Stable matching problem
給予n男和n女的偏好清單，找到stable matching若其存在。

設計演算法

basic ideas

一開始，所有人都沒結婚（unmarried），假設現在一男生m向其清單上排名最高的女生w求婚，可以直接將這兩人進行配對嗎？不一定。因為未來可能有w更喜歡的人m′（排名更高）向她求婚；但w也不能直接拒絕m，否則未來可能不會有比m排名更高的男生向其求婚。所以我們可以將其先放在中間狀態（intermediate state）—訂婚（engagement）。
現在處於「部分男生和女生是未訂婚（free），剩下是訂婚（engaged）」的狀態。下一步可能會像是，某一男生m向其清單上排名最高的女生w求婚，若w未訂婚，則和m訂婚；若w已和m′訂婚，則查看m和m′誰的順位較高，便和其訂婚。
最後當沒有任何人是free的時候，所有訂婚（engagement）狀態都會變成最終結果，也就是結婚!這樣的perfect matching就可以背回傳

Gale-Shapley algorithm

Initailly all m∈M and w∈W are free
while (there is a man m who is free and hasn't proposed to every woman)
{
    choose such a man m
    Let w be the highest-ranked woman in m's preference list to whom m hasn't yot proposed
    If (w is free)
    {
        (m,w) become engaged
    }
    Else //(w is currently engaged with m′)
    {
        If(w prefers m′ to m)
        {
            m remains free
        }
        Else //(w prefers m to m′)
        {
            (m,w) become engaged
            m′ becomes free
        }
    }
}
Return the set S of engaged pairs

依照上面的邏輯可以簡單地設計出演算法，但我們很難立即直接地看出這樣會是stable matching，甚至是perfect matching，所以接下來我們要一步步地證明及分析此演算法。

分析演算法

在證明較不直接可被觀察的事實前，我們會先列出幾項簡單的敘述：

一女生在被第一次求婚後會一直保持著「訂婚」的狀態，且她的對象只會有「愈變愈好」的可能。
一男生在向最喜歡的女生求婚後，可能「free」或「訂婚」，在這之後他的狀態也可能在這兩者間交換，且其對象僅有「愈變愈壞」的可能
G-S演算法最多會在while迴圈執行n^2次後結束
Proof :利用「衡量過程」的方式來證明每一步都會讓這個演算法更接近終結
每一個迴圈，都會有一些男生向他之前沒求婚過的女生求婚。讓P(t)表示在t迴圈時所有的pairs對數，我們知道，P(t+1)一定會大於P(t)，而最多只有n^2種可能的pairs組合，因此P(.)的值最多就是成長n^2次。得到最多就是n^2次迴圈
若在執行過程中有一男生是free，那必定有一女生是尚未被求婚的
Proof : 反證法 - 假設有一男生是free但已經對所有女生求婚過
男生m已向所有n個女生求婚，根據第一點可知，此時，所有n個女生都應該保持著訂婚狀態，而Pair須由相對應數量的男生(n個)組成，因此必定有n個男生已訂婚，而總共也只有n個男生，m未訂婚會跟假設矛盾。
最終的結果會是Perfect matching
Proof : 反證法 - 假設有一男生最後是free的
終結時，代表男生一定已經向所有女生求婚過，否則while會變成無窮迴圈，但這和第4點矛盾（若有男生是free代表一定有女生尚未被求婚）。
最終結果會是Stable matching
Proof : 反證法 - 假設結果不是stable
情境假設: 現在G-S演算法的結果是（m-w）（m′-w′），但有unstable的情況代表「m更喜歡w′勝過w且w′更喜歡m勝過m′」或另一種組合。
在G-S 演算法中，因為m喜歡w'更勝w，所以可知m是最後走向w求婚，但我們好奇，在m向w求婚前，是否有向w'求婚?
1. 沒有
  從「男生的配對會愈來愈壞」來看，m應該是喜歡w勝於w' 。矛盾
2. 有
  但考慮m最後是跟別人在一起，所以代表他被w'拒絕了，因為女生在free時不會拒絕，因此此時w'必定已和一男生m''配對，考慮以下兩種情形：
  1. m'' = m'
    w' 喜歡 m' 更勝於 m （所以拒絕ｍ）矛盾
  2. m'' ≠ m'
    ｗ'喜歡 m''更勝於m（所以拒絕ｍ），又最終結果是w'和m'配對，代表w'喜歡m'更勝於m''。可得w' 喜歡 m' 更勝於 m。矛盾

man-optimal
Proof : 反證法-假設不會men-optimal
情境假設：在第k天的時候才第一次發生某man被其optimal woman拒絕
符號化：在day k 時，M被W'拒絕 => （1）M的optimal woman是 W' （2）W' 是因為 M'才拒絕M
但因情境所說W' 終究是M的optimal woman，因此可說存在一組stable matching，其中M和W '是在一起的，我們稱此stable matching為T : （Ｍ－Ｗ'）（Ｍ'－Ｗ）。
現在要用反證法證明T根本是unstable。
首先，據（2）已知W '喜歡M'更勝於M。
再者，因為day k是第一次有人被其optimal woman拒絕的日子，故可知M'求婚當下並未有人被拒絕過，但daky k 時是因為W'更喜歡M'而拒絕M，所以M'非常有可能最愛W'（不排除M'在之前有被其他人拒絕過，只是那些都不是他的optimal woman，所以和day k的定義無關。），所以可知，W'至少和M'的optimal woman同等優先 => M'喜歡W'更勝於W'
兩處粗體字證明T根本不stable。
woman-pessimal
Proof : 假設不會woman pessimal
現有一pair S（Ｗ－Ｍ），且M並非W的pessimal woman，也存在另一個stable matching S'為（W-M'）（W'-M），其中W喜歡M勝過M'，但根據Man-optimal可知M是喜歡W勝過W'，因此S'根本不stable。矛盾

5 Representative Problems

Interval Scheduling

Given : 一堆附有起始、結束時間的工作集合（set of jobs with start times and finish times）

Goal :找到能達到最多工作且工作不重疊的子集合（find maximum cardinality subset of mutually compatible jobs）

e.g.為機檯安排工作，只有一台機器，要處理愈多工作愈好。如下表，共有T1~T10的時間段及A~G共7個工作的起始結束時間，要安排最多的工作，解答可以是{A,E,G}

A	A	A
	B	B
		C	C	C
		D	D	D	D	D
			E	E	E
				F	F	F	F
						G	G	G	G
T1	T2	T3	T4	T5	T6	T7	T8	T9	T10

Weighted Interval Scheduling

由上一個問題衍伸，但是將「完成最多工作」改成「使完成的工作可獲取最大利益」。在現實生活中，就像工廠不一定要做最多工作，而是優先去滿足可得到最大利益的工作們。

Given : 一堆附有起始、結束時間的工作集合（set of jobs with start times and finish times）

Goal :找到能使完成的工作可獲取最大利益且工作不重疊的子集合（find maximum cardinality subset of mutually compatible jobs）

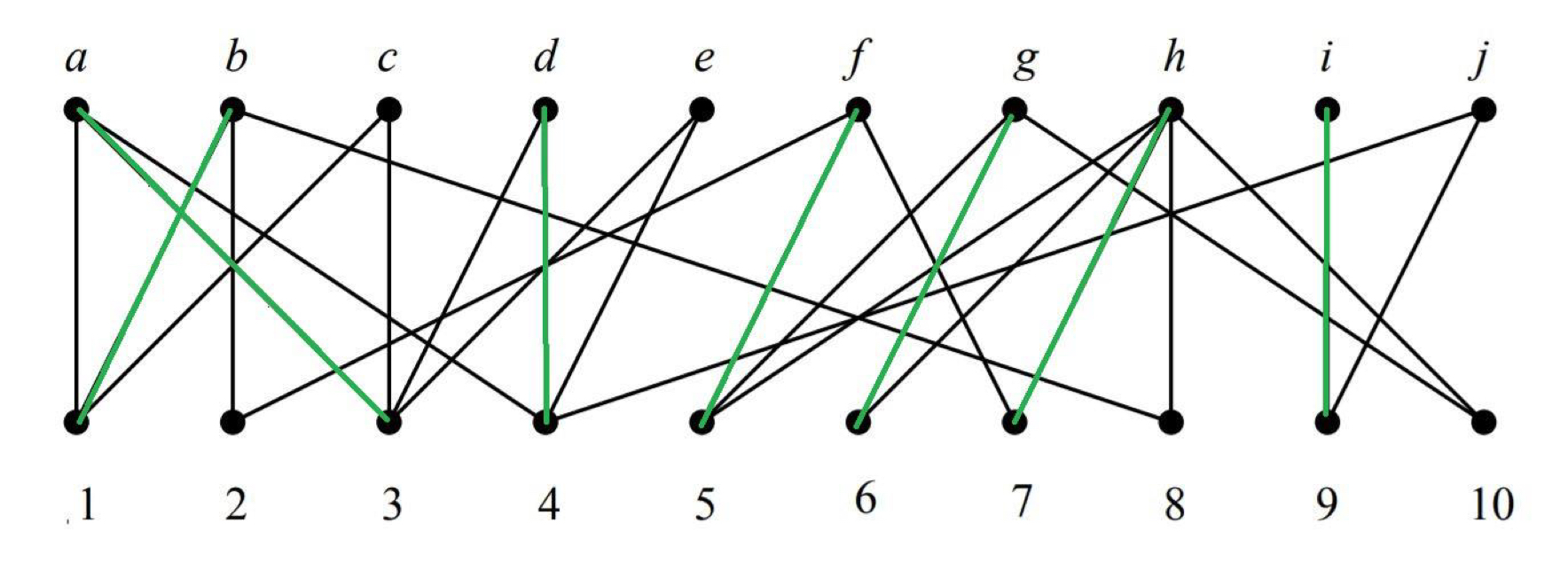
Bipartite Matching

e.g.像是配對愈多的業務人員和任務

Given : Bipartite graph

Goal : 最多的配對組合（find maximum cardinality matching）

Dominating Set and Independent Set

Given : graph

Goal :

Dominating set 是指在圖G=(V,E)中找到最少的點v滿足所有點都被連接的條件。
e.g.電信骨幹網路
Independent Set是指在圖G=(V,E)中找到最多的點v滿足，任意選擇的兩點間不可相連。
e.g.在你的朋友中找到最多人一起參加活動，但兩兩之間都不可是有交惡的
** Interval Scheduling 及 Bipartite Matching都可以被轉換為Independent Set的特例

下圖的(a)及(b)是Dominating set也是Independent Set；(c)僅是Dominating set

Competitve Facility Location

Given : 每節點都有權重的圖G（graph with weight in each node）

Rule :

兩競爭的玩家輪流選擇節點
不可選擇已被挑選節點的鄰邊節點

Goal :挑到有最大權重的子集合

下圖中第二位玩家最多保證可選到20而非25

Exercise

EX1

Q

根據以下情境進行matching：現有一小鎮，鎮上有n個男生及n個女生，其中n個男女生中各有k個好人及n-k個壞人，而每個男女生自己有異性的偏好順序清單，清單中的排序規則是好人順序一定優於壞人。請顯示在每個stable matching下，每個好男生都會和好女生配對。

A

Proof : 假設在現在的stable狀態下，有一好男生和壞女生配對

目前配對情況為一好男生和壞女生（Ｍ－Ｗ'），所以剩下（k-1）個好男生及（k）個好女生，因此必定會有一個好女生和壞男生搭配（M' - W）。但是根據好人順序一定優於壞人的原則，M一定喜歡W勝過W' ；W喜歡M勝過M' ，因此可說目前這樣的狀態根本不stable

EX2

Q

一般的Stable Matching Problem之下多增加一條件：某些配對組合是被禁止的。情境如下：有一集合M共有n個男生、集合W共n個女生，及一禁止配對集合F ⊆ M x W（F是所有男女不可配對的組合，且可能是所有的配對組合，若為⊂才表示一定小於配對數），所有男女生的排序清單都已排除不可配對的對象（例如 man m 會 rank all woman w , for (m,w) ∉ F）。在這樣的情境之下，我們說一個Stable Matching S 是stable，只要他不違反下列情況：

一般的instability
Pair（M-W）（M'-W'）而M喜歡W'勝過W；W'喜歡M勝過M'
有配對中的man更喜歡single woman
Pair（Ｍ－Ｗ）和單身的W'，而M喜歡W'勝過W
有配對中的woman更喜歡single man
Pair（Ｍ－Ｗ）和單身的M'，而W喜歡M'勝過M
有兩個不被禁止的男女單身 (m,w) ∉ F

注意，根據上述一般性定義，可知 一stable matching不一定要是 perfect matching。

我們的問題是「對於每一種偏好清單集合以及禁止配對集合，是否皆存在一stable matching？」用以下兩種方法之一回答此問題

對於此問題設計演算法
舉一反例說明某狀況下不存在stable matching

A

1.設計演算法

設計

在面對這樣類似的問題時，如果無法直接找到反例來說其不stable，我們可考慮直接採用G-S Algorithm，設計完後再進行分析，來驗證其是否stable。注意該演算法本來就沒有考慮有 被禁止的配對存在 這件事，然而我們並不希望man向所有的woman求婚，因此我們應該在while迴圈做些更動。演算法如下：

Initially all m ∈ M and w ∈ W are free
While there is a man who is free and hasn't proposed to every woman w for which (m,w)∉F
    Choose such a man m
    Let w be the highest-ranked woman in m's preference list to which m has not yet proposed
    If w is free then
        (m,w) become engaged
    Else w is currently engaged to m'
        If w prefers m' to m
            m remains free
        Else w prefers m to m'
            (m,w) become engaged
            m' becomes free
        Endif
    Endif
Endwhile
Return the set S of engaged pairs

分析

我們根據原先分析G-S演算法的方式進行

此演算法仍為O(n^2)
男生的對象有愈變愈差（女生的對象愈變愈好）的結果仍存在
我們不必擔心不會產生perfect matching （事實上，真的可能不會）
若有男生單身代表他必定向所有不被禁止的女生求婚過；若女生單身，代表沒有男生向她求婚過

最後，我們要證明的是「最後回傳的matching S 不會unstable」

Proof : 共有四種不穩定的情形，我們只要確保不違反即可

一般的instability - Pair（M-W）（M'-W'）而M喜歡W'勝過W；W'喜歡M勝過M'
M必定向W'求婚過但沒再一起表示被拒絕了，代表W'喜歡M'更勝於M，矛盾。
有配對中的man更喜歡single woman - Pair（Ｍ－Ｗ）和單身的W'，而M喜歡W'勝過W
M必定向W'求婚過，但W是單身代表她未被求婚過，矛盾。
有配對中的woman更喜歡single man - Pair（Ｍ－Ｗ）和單身的M'，而W喜歡M'勝過M
M'必定向W求婚過但被拒絕了，代表W喜歡M更勝於M'，矛盾。
有兩個不被禁止的男女單身 (m,w) ∉ F
男生M一定會向所有不被禁止的女生求婚，但女生W仍然單身，矛盾。

2.不存在stable matching的例子

因為我們已在上一部份證明其必定會stable，所以這裡就不用了，耶~

EX3

Q

True （give a short explanation）or False（give a counterexample反例）？

在每一個Stable Matching Problem都存在一pair （Ｍ－Ｗ）其中，W是M的最高順位者，且M是W的最高順位者。

A

False

例子如下表 :

Man's preference list	1st	2nd
M	W	W'
M'	W'	W

Woman's preference list	1st	2nd
W	M'	M
W'	M	M'

EX4

Q

True （give a short explanation）or False（give a counterexample反例）？

考慮一Stable Matching Problem，若有存在Pair（Ｍ－Ｗ）且MW互相為彼此的第一順位，是否這些pair（Ｍ－Ｗ）都是stable matching？

A

Proof : 假設（Ｍ－Ｗ）unstable

代表存在另兩Pair（Ｍ－Ｗ'）（Ｍ'－Ｗ）是stable，且M 喜歡 W更勝於W'；W喜歡M更勝於M'，根本不stable。矛盾。

EX5

Q

有兩家片商AB要爭奪某電視台一天之中的播放時段（ｎ個），且兩片商皆有ｎ個節目，電視台的選擇辦法是：「片商ＡＢ將其手中n個節目排序產生schedule S 和 T，再將 S 和 T兩者同時段的節目觀眾評分相比，選擇分數較高者放映。」在此題目中類似G-S問題中的stability定義為「兩片商都沒有其他安排方式（產生schedule S’ 和 T’）可使自身得到更多放映時間」。考慮任何節目數量及其評分是否可產生stable schedule？

用以下兩種方法之一回答此問題

對於此問題設計演算法
舉一反例說明某狀況下不存在stable matching

Ａ

舉一反例說明某狀況下不存在stable matching。

假設現在的情況: ｎ＝２且片商Ａ的兩節目｛a1,a2｝及其評分為｛20,40｝；片商B的兩節目｛b1,b2｝及其評分為｛10,30｝:排出以下時間表

｛a1(20), a2(40)｝｛b1(10), b2(30)｝: B會希望交換b1,b2使其至少贏下一時段。
｛a1(20), a2(40)｝｛b2(30), b1(10)｝: A會希望交換a1,a2使其贏下兩時段而非一時段。

EX6

Q

在G-S演算法於1962年發明前，此演算法的概念已被用在另一問題上，該問題是關於「醫院招聘住院醫師」，情境如下：有m間醫院，每間都有住院醫師職位空缺（＞１），而有n名醫學生會畢業投入醫院，醫院及醫學生都有自己的偏好順序清單，且n的數量大於所有m間醫院的職位空缺總和。和G-S問題一樣，要進行配對，且因為學生較多，必定會有學生沒有被分配到醫院，只要不是下面兩種狀況就說是stable：（S為Student、H為Hospital）

S被指派給H，S'未被指派，但H較喜歡S'勝過S
像一般的unstable，（S-H）（S'-H'）但S喜歡H'勝過H；H'喜歡S'勝過S

設計演算法並分析其說明總是會是stable assignment。

A

設計

A student is either "committed " to a hospital or "free"

Initially all hospital's position are empty and all students are not assigned to any hospital
while some hospital has available positions
    choose such a hospital h
    let s be the highest ranked student in the hospital's preference list to which hospital has not yet offers a position
    if s is free then
        s accepts the offer
    else s is currently committed to h'
        if s prefer h' to h then
            s remains committed to h'
        else s prefer h to h' then
            the number of available positions at h' increase by one
            the number of available positions at h  decrease by one

return the set J of assignments

分析

O(mn)
Proof : assignments is stable
假設assignments不stable，如題目所述會有兩種情況
1. S被指派給H，S'未被指派，但H較喜歡S'勝過S
  因為H會依照喜好順序問下去，代表S是H最後問的，那在這之前是否有問過S'
  1. 沒有 - 代表H喜歡S勝過S' 。矛盾。
  2. 有 - 代表S'已經committed to H' 而拒絕H，代表S'最終不可能是free的。矛盾。
2. 像一般的unstable，（S-H）（S'-H'）但S喜歡H'勝過H；H'喜歡S'勝過S
  因為H會依照喜好順序問下去，代表S是H最後問的，那在這之前是否有問過S'
  1. 沒有 - 代表H喜歡S勝過S' 。矛盾。
  2. 有 - 代表S'已經committed to H'' 而拒絕H
    1. H''==H'，代表S'喜歡H'勝過H所以拒絕H。矛盾。
    2. H''≠H'，S'最終是指派給H'，代表S'喜歡H'勝過H''而H''又勝過H，所以代表S'喜歡H'勝過於H。矛盾。

[1]Intro : Some Representative problems

Stable Matching​

問題描述​

如果你是月老...​

Stable​

stable matching不一定只有一種組合​

名詞定義​

設計演算法​

basic ideas​

Gale-Shapley algorithm​

分析演算法​

5 Representative Problems​

Interval Scheduling​

Weighted Interval Scheduling​

Bipartite Matching​

Dominating Set and Independent Set​

Competitve Facility Location​

Exercise​

EX1​

Q​

A​

EX2​

Q​

A​

1.設計演算法​

設計​

分析​

2.不存在stable matching的例子​

EX3​

Q​

A​

EX4​

Q​

A​

EX5​

Q​

Ａ​

EX6​

Q​

A​

設計​

分析​